Conway's Life x 262,144

Project Vision

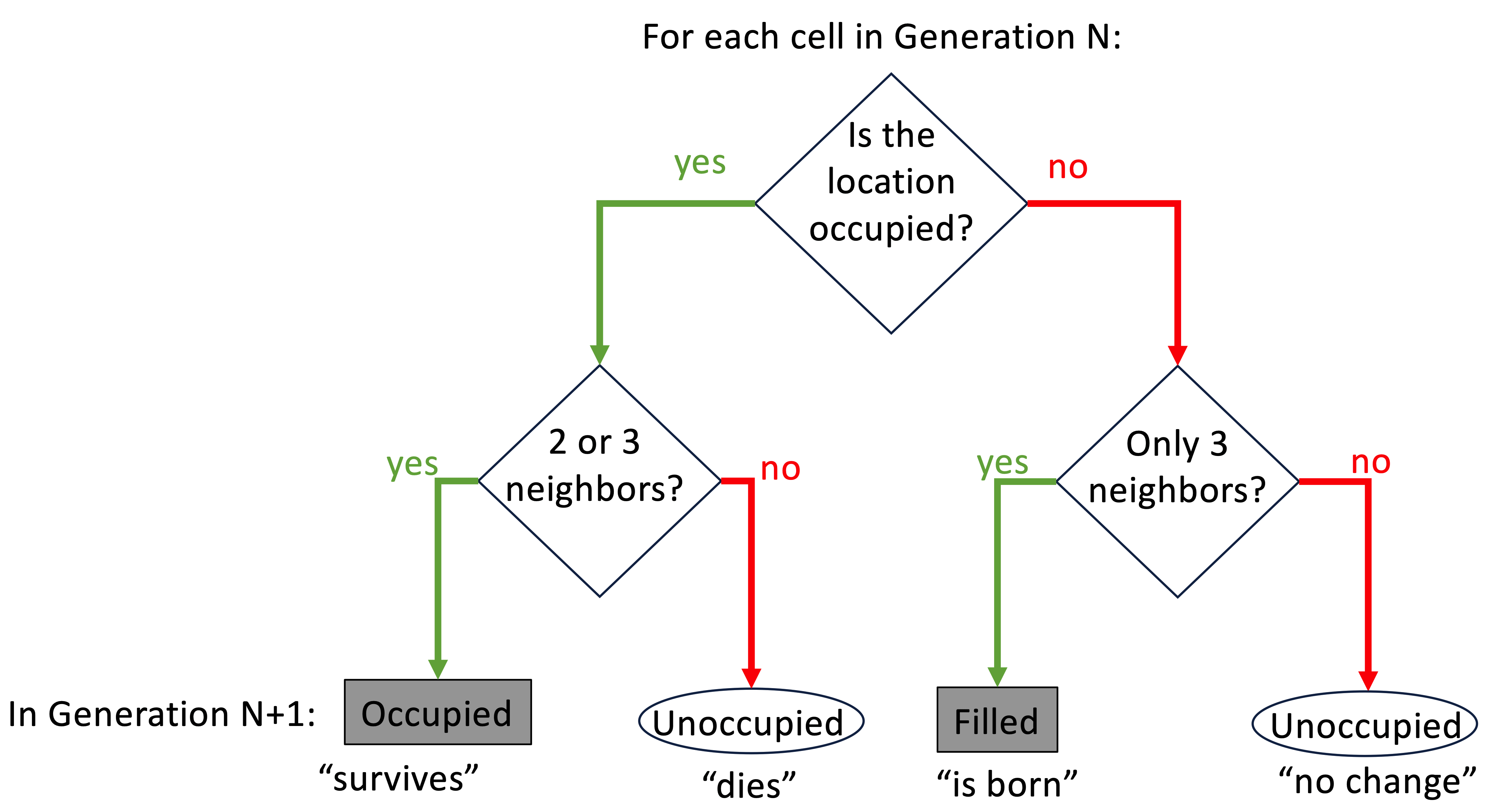
In 1970, John Conway described a mathematical game involving cellular automata that cane to be caled "Conway's Game of Life". It is played on a rectangular matrix of arbitrary size. The playing pieces are cells that each occupy one location in the matrix. In the game, cells can persist, die or be born from one generation to the next. The presence or absence of a given cell in the next generation depends only on how many neighbors that location has in the current generation. In a rectangular matrix, each location has between zero and eight neighbors:

Conway’s rules are:

A cell can persist into the next generation if it has two or three neighbors. Cells with fewer neighbors “die of loneliness”; cells with more neighbors “die of overcrowding”.
A cell can be born into an empty location in the next generation if that cell has exactly three neighbors.

Conway selected these rules after a period of experimentation to meet the following criteria:

There should be no initial pattern for which there is a simple proof that the population can grow without limit.
There should be initial patterns that apparently do grow without limit.
There should be simple initial patterns that grow and change for a considerable period of time before coming to end in three possible ways: fading away completely (from overcrowding or becoming too sparse), settling into a stable configuration that remains unchanged thereafter, or entering an oscillating phase in which they repeat an endless cycle of two or more periods.

In the original 1970 version, the game was played with physical checkers on a checkerboard.

In principle, the game could be played with other rules. I was interested to create an implementation of this where one could explore all the possible "rule sets".

262,144 Possible Sets of Rules

The original rules of the Game of Life can be described in brief: a cell survives if it has 2 or 3 neighbors, otherwise, it dies; a cell will be born into an empty location with exactly three neighbors. This is shown below:

These same rules can also be shown like this where a 1 in the rule indicates a occupied location in the next generation (survival or birth) for that number of neighbors and a 0 in the rule indicates an unoccupied location in the next generation (death or remaining empty).

I realized that you could encode the rules in an 18-bit binary number (see sidebar for details). Each of the low order nine bits (0 to 8) give the state of the location in the next generation (1 = occupied; 0 = unoccupied) for an unoccupied location with zero to eight neighbors – bit 0 gives the state in the next generation if the location currently has has zero neighbors; bit 1 for one neighbor; etc. Similarly, the high order nine bits (9 to 17) give the state of the next generation for an occupied location with zero to eight neighbors – bit 9 for zero neighbors; bit 10 for one neighbor; etc. Using this encoding, it is possible to specify any set of rules that are based on the number of neighbors a location has.

The bit pattern specifies the state of the cell in the next generation; the index into the bit pattern is the number of neighbors combined with whether the cell is currently occupied or not.

Shown below is the decoding of the rule 256020 as an example:

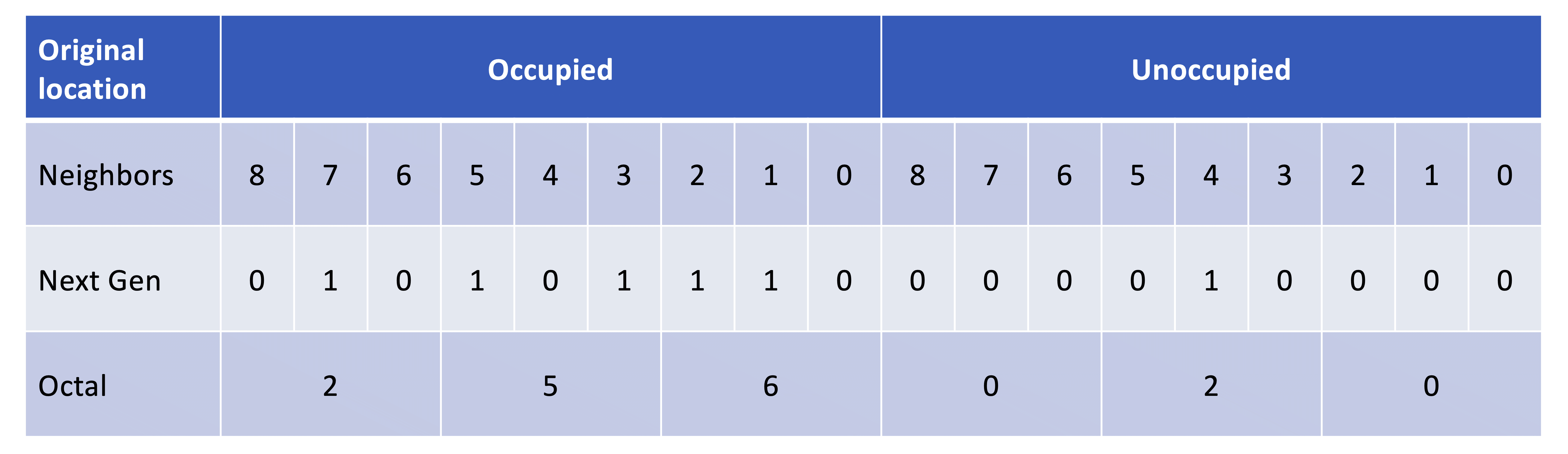
Translated into text, this would become:

Currently living cells survive if they have 1, 2, 3, 5, or 7 neighbors; otherwise, they die.
A cell will be born into each currently unoccupied location that has exactly 4 neighbors.

Interestingly, there is no need for these rules to “make biological sense”. For example, rule set 256020, where cells persist if they have 1, 2, 3, 5, or 7 neighbors. This rule set gives interesting behavior even though there’s no biological reason why 4, 6, and 8 neighbors would be overcrowded but 3, 5, and 7 would not.

Since all possible rule sets can be encoded in 18 binary bits and 2^18 = 262,144, this means there are 262,144 ways to play the GoL. This makes it possible to build a device that would allow a user to explore all of these possibilities and observe how a population of each different “species” would develop over time.

Practical Realization

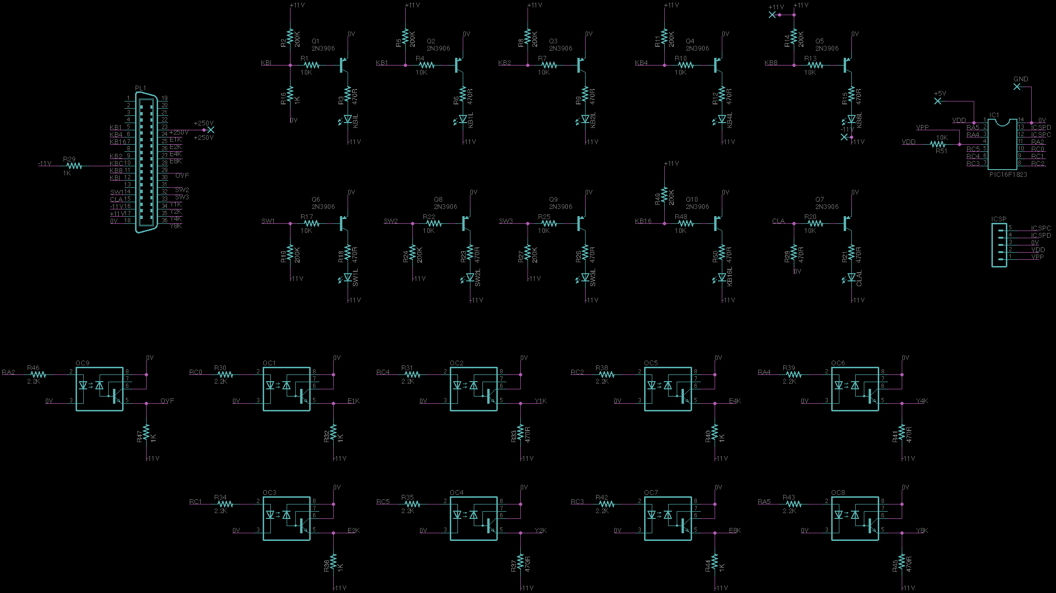
I implemented this using a 32x64 tri-color LED matrix and the Matrix Portal MCU from Adafruit.

The code was adapted from sample Game of Life code with the following modifications:

Color-coding: In Conway's original version, a cell is either alive or dead. This would map to just two colors: occupied (a color) and unoccupied (black). To make it more visually interesting, I modified this to add two other colors:

Unoccupied cells are black
Newborn cells are blue
If a cell persists for more than one generation, it is green
If a cell dies, it is a "ghost" for one generation; "ghosts" are purple

Setting the Rules: I used two sets of three binary encoded thumbwheel switches to set the 6 octal digits of the current rule set:

The top three digits specify the rules for occupied locations; thus, the rules for which cells survive to the next generation.
The middle three digits specify the rules for unoccupied locations; thus, the rules for birth of new cells.

Other Parameters: I added a bottom set of three thumbwheel switches to set other run parameters:

The left digit specifies the density of organisms in the initial population; specifically, the chance of any location being occupied at the start is 10%-times the setting of this thumbwheel. Thus, a setting of “3” means the world starts roughly 30% filled with cells. Since some rule sets give more interesting results with more or fewer occupied locations, this allows exploration of the effects of varying initial cell density.
The center digit specifies the number of generations to run before re-starting. For this, I chose an exponential scale to allow a wide range of run lengths. Specifically, it runs 2 * 10^(N/2) generations; thus, a setting of 4 would run for 200 generations. Some patterns resolve quickly while others never resolve; this control helps to keep the display in an interesting state.
Finally, the rightmost digit specifies the delay in seconds between generations; thus, a setting of 0 runs at maximum speed. Slowing down the generations makes it possible to follow the rules in detail if desired.

Results

This shows Conway's "standard" rules - 014010 in octal.

Since there are 262,144 different rule sets, we haven't had time to explore them all. I've been making a collection on YouTube.

Here are some interesting ones:

703703

016012

414610

720720